| Announcements |
|---|
| Key Facts | |
|---|---|
| Contact | Prof. Dr. rer. nat. Matthias Gerdts (UniBwM) Tuğba Akman, M.Sc. Felix Schweighofer, M.Sc. |
| Language of Instructions | English or German, depending on the audience |
| Language of Materials | English |
| Type / ECTS | Lecture, Exercise / 3 (Elective Lecture Module) |
| Semester | Summer Semester |
| Time and Place | Thursdays, 14:30-17:00, room MW3618 (TUMonline/Lecture, TUMonline/Exercise) Note: Lecture and exercise elements will be interspersed throughout the course session from 14:30 to 17:00. Note: The last regular course appointment will be already on 2024-06-27 to accommodate participants from UniBw M. Note: The additional Matlab exercise, formerly offered from 17:00 to 18:30, is canceled in favor of the Optimal Control Lab in the winter term. |
| Related Links | TUMonline: Lecture, Exercise |
| Details | |
|---|---|
| Prerequisites |
|
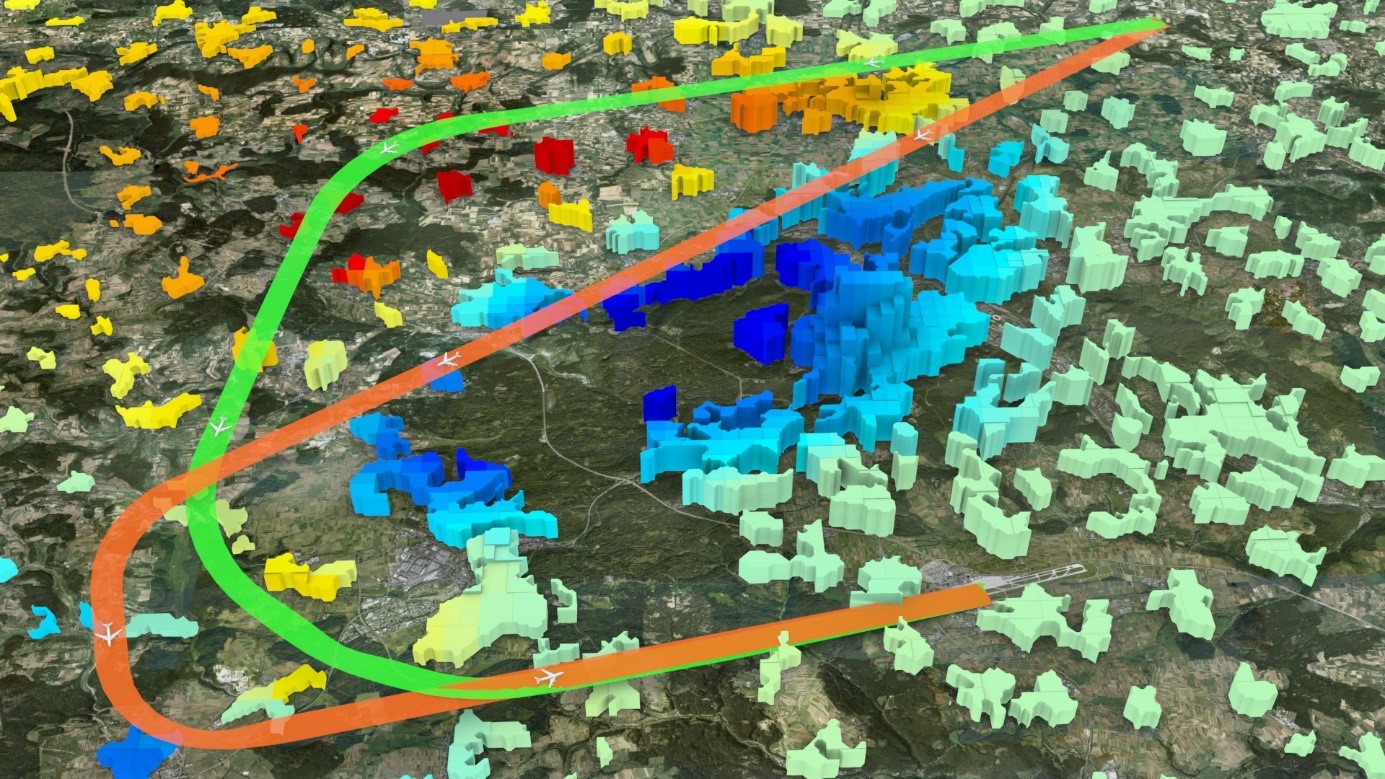
| Content / Educational Objectives | Aircraft trajectory optimization belongs to the mathematical field of optimal control. This means that the optimal control history and the optimal state history (and maybe other additional parameters) that minimize a given cost function for a given dynamic system need to be calculated. Thereby, all given initial and final boundary conditions as well as path equality and inequality constraints need to be fulfilled. This enables e.g. the calculation of noise minimal approach and departure trajectories for a given aircraft at a given airport considering the population distribution as well as any procedural requirements. In this lecture the students should learn how to solve such optimal control problems beginning with the modeling of the required dynamic system as well as the cost and constraint functions. In the next steps on the one side theoretical optimality conditions are derived for simple examples and on the other side discretization techniques for the solution of realistic problems are introduced. Afterwards, methods for the solution of the resulting sparse parameter optimization problem are presented. Finally, other aspects related to the implementation are introduced.
Table of Contents:
|
| Teaching Methods / Materials | For the lecture and the guided tutorial lecture notes are made available. The theory can be deepened in a MATLAB computer tutorial, guided by FSD.
For more detailed programming lessons, please consider the associated Optimal Control Lab during the winter semester. |
| Exam | Oral exam, 30 Minutes. Exam appointments will be arranged in coordination with the course participants and may take place at TUM (Garching) or UniBw M (Neubiberg). |
| Reference Literature |
|
This lecture is part of the Munich Aerospace Teaching Collaboration between TUM and UniBw M.